Table of Contents
Effect of nuclear weapons on historic trends in explosives
Published 31 December, 2014; last updated 10 December, 2020
Nuclear weapons constituted a ~7 thousand year discontinuity in relative effectiveness factor (TNT equivalent per kg of explosive).
Nuclear weapons do not appear to have clearly represented progress in the cost-effectiveness of explosives, though the evidence there is weak.
Details
This case study is part of AI Impacts’ discontinuous progress investigation.
Background
The development of nuclear weapons is often referenced informally as an example of discontinuous technological progress. Discontinuities are sometimes considered especially plausible in this case because of the involvement of a threshold phenomenon in nuclear chain reactions.

Trends
Relative effectiveness factor
The “relative effectiveness factor” (RE Factor) of an explosive measures the mass of TNT required for an equivalent explosion.2
Data
We collected data on explosive effectiveness from an online timeline of explosives and a comparison of RE factors on Wikipedia.3 These estimates modestly understate the impact of nuclear weapons, since the measured mass of the nuclear weapons includes the rest of the bomb while the conventional explosives are just for the explosive itself.
Figures 1-3 below show the data we collected, which can also be found in this spreadsheet. Our data below is incomplete– we elide many improvements between 800 and 1942 that would not affect the size of the discontinuity from “Fat man”. We have verified that there are no explosives with higher RE factor than Hexanitrobenzene before “Fat man” (see the ‘Relative effectiveness data’ in this spreadsheet for this verification).
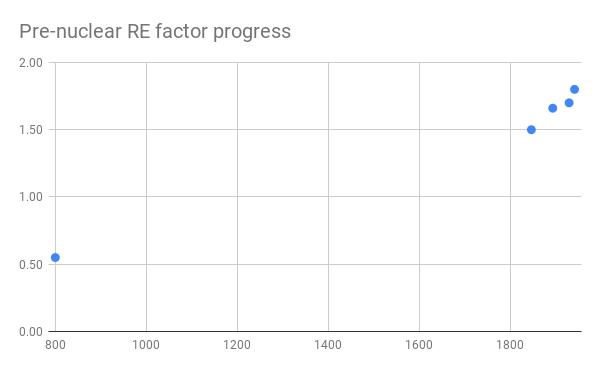
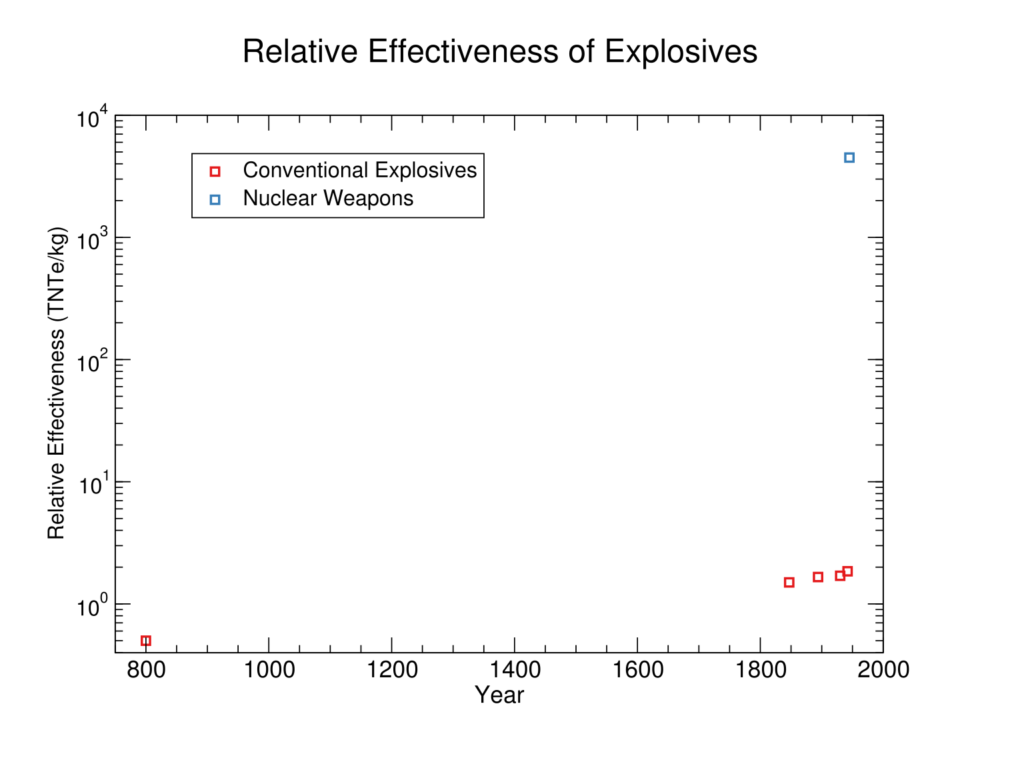
Discontinuity Measurement
To compare nuclear weapons to past rates of progress, we treat progress as exponential.4 With this assumption, the first nuclear weapon, “Fat man”, represented a around seven thousand years of discontinuity in the RE factor of explosives at previous rates.5 In addition to the size of this discontinuity in years, we have tabulated a number of other potentially relevant metrics here.6
We checked if “Fat Man” constituted a discontinuity, but did not look for other discontinuities, because we have not thoroughly searched for data on earlier developments. Even though we’re missing data, since gunpowder is the earliest known explosive and Hexanitrobenzene is the explosive before “Fat man” with the highest RE factor, the missing data should not affect discontinuity calculations for “Fat man” unless it suggests we should be predicting using a different trend. This seems unlikely given that early explosives all have an RE factor close to that of our existing data points, around 1 – 3 (see table here)7, so are not vastly inconsistent with our exponential. If we instead assumed a linear trend, or an exponential ignoring the early gunpowder datapoint, we still get answers of over three thousand years (see spreadsheet for calculations).
Discussion of causes
Interestingly, at face value this discontinuous jump does not seem to be directly linked to the chain reaction that characterizes nuclear explosions, but rather to the massive gap between the energies involved in chemical interactions and nuclear interactions. It seems likely that similar results would obtain in other settings; for example, the accessible energy in nuclear fuel enormously exceeds the energy stored in chemical fuels, and so at some far future time we might expect a dramatic jump in the density with which we can store energy (though arguably not in the cost-effectiveness).8
Cost-effectiveness of explosives
Another important measure of progress in explosives is cost-effectiveness. Cost-effectiveness is particularly important to understand, because some plausible theories of continuous progress would predict continuous improvements in cost-effectiveness much more strongly than they would predict continuous improvements in explosive density.
Data
= Cost-effectiveness of nuclear weapons =
Assessing the cost of nuclear weapons is not straightforward empirically, and depends on the measurement of cost. The development of nuclear weapons incurred a substantial upfront cost, and so for some time the average cost of nuclear weapons significantly exceeded their marginal cost. We provide estimates for the marginal costs of nuclear weapons, as well as for the “average” cost of all nuclear explosives produced by a certain date.
We focus our attention on WWII and the immediately following period, to understand the extent to which the development of nuclear weapons represented a discontinuous change in cost-effectiveness.
See our spreadsheet for a summary of the data explained below. According to the Brookings Institute, nuclear weapons were by 1950 considered to be especially cost-effective (though not obviously in terms of explosive power per dollar), and adopted for this reason. However, Brookings notes that this has never been validated, and appears to distrust it.9 This disagreement weakly suggests that nuclear weapons are at least not radically more or less cost-effective than other weapons.
According to Wikipedia, the cost of the Manhattan project was about $26 billion (in 2014 dollars), 90% of which “was for building factories and producing the fissile materials.”10 The Brookings U.S. Nuclear Weapons Cost Study Project estimates the price as $20 billion 2014 dollars, resulting in similar conclusions.11 This post claims that 9 bombs were produced through the end of “Operation Crossroads” in 1946, citing Chuck Hansen’s Swords of Armageddon.12 The explosive power of these bombs was likely to be about 20kT, suggesting a total explosive capacity of 180kT. Anecdotes suggest that the cost to actually produce a bomb were about $25M,13 or about $335M in 2014 dollars. This would make the marginal cost around $16.8k per ton of TNT equivalent ($335M/20kT = $16.75k/T), and the average cost around $111k/T.
In 2013 the US apparently planned to build 3,000 nuclear weapons for $60B.14 However it appears that at least some of these may be refurbishments rather than building from scratch, and the B61-12 design at least appears to be designed to be less powerful than it could be, since it is less powerful than the bombs it is replacing15 and much less powerful than a nuclear weapon such as the Tsar Bomba, with a yield of 50mT.16 The B61-12 is a 50kT weapon. These estimates give us $400/T ($60B/3,000*50kT). They are very approximate, for reasons given. However have not found better estimates. Note that they are for comparison, and not integral to our conclusions.
These estimates could likely be improved by a more careful survey, and extended to later nuclear weapons; the book Atomic Audit seems likely to contain useful resources.17
| Year | Description of explosive | Cost per ton TNT equivalent |
| 1920 | Ammonium nitrate | $5.6k |
| 1920 | TNT | $10.5k |
| 1946 | 9 (Mark 1 and Mark 3’s) x 20kt (marginal) | $16.8k (marginal Mark 3) |
| 1946 | 9 (Mark 1 and Mark 3’s) x 20kt (average) | $111k (average Mark 3) |
| 3,000 weapons in the 3+2 plan | $400 |
Table 2: Total, average and marginal costs associated with different weapons arsenals
= Cost-effectiveness of non-nuclear weapons =
We have found little information about the cost of pre-nuclear bombs in the early 20th Century. However what we have (explained below) suggests they cost a comparable amount to nuclear weapons, for a certain amount of explosive energy.
Ammonium nitrate and TNT appear to be large components of many high explosives used in WWII. For instance, blockbuster bombs were apparently filled with amatol, which is a mixture of TNT and ammonium nitrate.18
An appropriations bill from 1920 (p289) suggests that the 1920 price of ammonium nitrate was about $0.10-0.16 per pound, which is about $1.18 per pound in 2014.19 It suggests TNT was $0.44 per pound, or around $5.20 per pound in 2014. These estimates are consistent with that of a Quora commenter.20
This puts TNT at $10.4k/ton: very close to the $16.8k/ton marginal cost of an equivalent energy from Mark 3 nuclear weapons, and well below the average cost of Mark 3 nuclear weapons produced by the end of Operation Crossroads.
Ammonium nitrate is about half as energy dense as TNT, suggesting a price of about $5.6k/T.21 22 This is substantially lower than the marginal cost of the Mark 3.
Note that these figures are for explosive material only, whereas the costs of nuclear weapons used here are more inclusive. Ammonium nitrate may be far from the most expensive component of amatol-based explosives, and so what we have may be a very substantial underestimate for the price of conventional explosives. There is also some error from synergy between the components of amatol.23
Discontinuity Measurement
Without a longer-run price trend in explosives, we do not have enough pre-discontinuity data to measure a discontinuity.24 However, from the evidence we have here, it is unclear that nuclear weapons represent any development at all in cost-effectiveness, in terms of explosive power per dollar. Thus it seems unlikely that nuclear weapons were surprisingly cost-effective, at least on that metric.
Notes
- From Wikimedia Commons: U.S. Army Photographic Signal Corps [Public domain]
“TNT Equivalent.” Wikipedia. June 26, 2019. https://web.archive.org/web/20190626194926/https://en.wikipedia.org/wiki/TNT_equivalent- See our methodology page for more details.
- See our methodology page for more details.
- See this blog post for a discussion of why nuclear weapons were such a large discontinuity.
- “Some observers believe the absence of a third world war confirms that these weapons were a prudent and cost-effective response to the uncertainty and fear surrounding the Soviet Union’s military and political ambitions during the cold war. As early as 1950, nuclear weapons were considered relatively inexpensive— providing “a bigger bang for a buck”—and were thoroughly integrated into U.S. forces on that basis. Yet this assumption was never validated. Indeed, for more than fifty years scant attention has been paid to the enormous costs of this effort—more than $5 trillion thus far—and its short and long-term consequences for the nation.”
Schwartz, Stephen I., and Stephen I. Schwartz. “Atomic Audit.” Brookings. October 23, 2018. Accessed July 02, 2019. https://www.brookings.edu/book/atomic-audit/. - “The next definite data in Swords of Armageddon gives bomb production up to the end of the 1946 Operation Crossroads: total bombs built 9, total bombs detonated 5, bombs remaining in stockpile 4. “
“How Many Atomic Bombs Were Made during Ww2.” Answers. Accessed July 02, 2019. https://www.answers.com/Q/How_many_atomic_bombs_were_made_during_ww2.
“Index.htm.” Index.htm. Accessed July 02, 2019. http://www.uscoldwar.com/. - “Just before take-off, Admiral Purnell asked Sweeney if he knew how much the bomb cost. Sweeney answered, ‘About $25 million.’ Purnell then warned him, ‘See that we get our money’s worth.'” – “Wayback Machine”. 2019. Web.Archive.Org. Accessed July 5 2019. https://web.archive.org/web/20150406054646/http://www.mputtre.com/sitebuildercontent/sitebuilderfiles/copy_of_tinian_fat_man_speech.pdf.
- “Ultimately, the plan calls for some 3,000 of these new weapons at an estimated cost of $60 billion, or $20 million each.”
“How Much Does It Cost to Create a Single Nuclear Weapon?” Union of Concerned Scientists. Accessed July 02, 2019. https://www.ucsusa.org/publications/ask/2013/nuclear-weapon-cost.html#.VKNkUIrF8kM. - “The new Air Force bomber would carry two types of nuclear weapons: a rebuilt gravity bomb (the B61-12) and a cruise missile, known as the Long-Range Stand-Off (LSRO) weapon or Air-Launched Cruise Missile (ALCM)” “The B61-12 would have a maximum yield of up to 50 kilotons, but would replace a bomb (the B61-7) with a yield of up to 360 kilotons. “
“Projects & Reports.” SECTION 1: Nuclear Reductions Save Money | Arms Control Association. Accessed July 02, 2019. https://www.armscontrol.org/reports/The-Unaffordable-Arsenal-Reducing-the-Costs-of-the-Bloated-US-Nuclear-Stockpile/2014/10/Section_one. - “Blast yield50 megatons of TNT (210 PJ)[2]“
“Tsar Bomba.” In Wikipedia, October 24, 2019. https://en.wikipedia.org/w/index.php?title=Tsar_Bomba&oldid=922820257.
- ”
Amatol was used extensively during World War I and World War II, typically as an explosive in military weapons such as aircraft bombs, shells, depth charges, and naval mines.”
“Amatol.” Wikipedia. May 25, 2019. Accessed July 02, 2019. https://en.wikipedia.org/wiki/Amatol. - “For example, as was explained yesterday, TNT will cost on an average 44 cents a pound, whereas ammonium nitrate will run from, say, 10 to 15.5 cents…” General Deficiency Bill, 1918: Hearings Before Subcommittee of House Committee on Appropriations … in Charge of Deficiency Appropriations for the Fiscal Year 1917 and Prior Fiscal Years, Sixty-fifth Congress, Second Session. Accessed online at
- See our methodology page for more details.

