Table of Contents
Chaos in Humans
Published 31 March, 2023. Last Updated 31 March, 2023.
Both chaotic and non-chaotic dynamics occur in humans at all scales, from molecules to societies.
Details
Background
If humans are chaotic, then our long-time behavior is inherently unpredictable. Not even a superintelligence would be able to reliably predict the behavior of a particular human.
The strong version of this claim is clearly false: there are some things that we can predict about human behavior, even long in advance. We expect these to be associated with non-chaotic dynamics in the brain. The weak claim is more interesting. Does there exist some dynamics in the human brain which is chaotic? Are there some aspects of human behavior that are inherently unpredictable?
The answer is less clear than we had hoped at the beginning of the investigation, but it seems as though chaos is at least possible on all or almost all of the scales relevant to human behavior.
There are various scales on which humans might be chaotic. At the largest scales, are human societies chaotic? At the human scale, how chaotic or predictable is an individual’s behavior? At the organ scale, how chaotic is the human brain? Other organs might also exhibit chaos, but it seems less likely that chaos in the endocrine system, for example, would be as important for understanding human behavior as chaos in the brain. At the cellular scale, do individual neurons behave chaotically? At the atomic and molecular scales, thermal noise and quantum effects dominate. This is not classical chaos, but it does provide the microscopic uncertainty that might be amplified by the chaos at larger scales.
It seems as though, at most scales, there can be either chaotic or non-chaotic behavior, and there can be transitions between the two.1) This makes it difficult to determine if there is a continual chain of chaos from atomic to macroscopic scales. Even though this is hard to show, it seems likely that this would be true for at least some important sub-system of the brain in some circumstances. Chaos is a thing that a brain can do, even if not everything the brain does is chaotic.
Even if humans are not predictable, we might still be controllable. In order for you to control a chaotic system, it has to be possible to input a signal of the same sort as any of the sources of uncertainty that the chaos amplifies, and at a speed faster than the Lyapunov time. Whenever the trajectory starts to diverge from the path through the chaos you want it to follow, you have to input some signal to correct the path, before the divergence has gotten too large.
If thermal or quantum uncertainty inside the brain were amplified by chaos at all scales, then it would become macroscopically important. This would imply that humans are uncontrollable as well as chaotic, because the signal you would need to input to correct for this uncertainty would be something atomic-scale somewhere inside the brain. If there were instead some intermediate mesoscale which were not chaotic, then it would be possible to average over the chaos at smaller scales (such as over atoms or proteins) to get a predictable result (e.g. at the level of neural firing). This would shield any macroscopic chaos from the internal microscopic sources of uncertainty. The important sources of uncertainty would then be from the external environment, which is potentially controllable by an external actor - unless the external environment is itself unavoidably chaotic and uncontrollable.
This page largely follows a review article from 2003 by Korn & Faure, supplemented with more recent evidence, which discusses experimental evidence for chaos in the brain at various scales.2)
Atoms
Motion at the atomic scale is dominated by quantum and thermal uncertainties. Figuring out which state a wavefunction will collapse into, or which Everett branch should be expected in the future, is a currently unsolved and potentially unsolvable problem. Even without considering quantum mechanics, detailed knowledge of the thermal motion of atoms allows you to violate the Second Law of Thermodynamics. For example, Maxwell’s demon stands at a narrow gate between two containers of gas. By measuring the velocity of atoms approaching the gate and selectively opening and closing the gate to allow only some of them through, Maxwell’s demon can transfer temperature and pressure between the two gasses without doing any work.3) If we assume that a superintelligence is subject to the Second Law of Thermodynamics, then it cannot measure and predict the details of classical atomic motion, much less quantum motion.
Macromolecules
This is a scale we know relatively little about, so we welcome comments from anyone with more expertise.
Macromolecules, like proteins or lipids, are large enough that they are not directly affected by quantum and thermal effects. The question is whether there exist some important macromolecules in the brain which amplify quantum or thermal uncertainty to larger scales. There seem to be a few examples from elsewhere in biology where this is the case.4)
In order for photosynthesis to convert sunlight into chemical energy, light has to first be absorbed by a structure which acts as an antenna, then the excitation has to be transferred to a reaction center, where it can be used for charge separation. This transfer of the excitation occurs with almost perfect efficiency; it is more efficient than is possible classically. Instead, quantum coherence helps the electron find the quickest path to the reaction center, despite the warm and wet biological setting.5)
Some bird species can sense the earth’s magnetic field and use it to navigate.6) The mechanism seems to involve quantum spin states of pairs of electrons.7) In a bird’s retina, there are some pigments (cryptochromes) which absorb light and separate electrons into a radical pair. The spins of the electrons are initially pointing in opposite directions (in a singlet state), but an external magnetic field can flip them so they point in the same direction (in a triplet state). The decay products of the singlet and triplet are different. The retina can detect how the relative concentration of the decay products changes, allowing the bird to “see” the magnetic field. The energy difference between the two states is associated with a frequency of 1-100 MHz.8) Exposing a bird (European robin) to a weak magnetic field oscillating at this frequency disorients it, so it is unable to navigate. This sense requires maintaining quantum coherence of the spins for at least 100 microseconds, longer than the best man-made spin states in similarly warm and wet environments.9)
A few other biological quantum processes have been proposed, although they do not seem to have gained as broad of acceptance as these two. Electron transfer over tens of angstroms between redox centers in proteins might occur via tunneling,10) including possible interference between different paths.11) Biological photoreceptors can be extremely sensitive to small amounts of light. Rods in human eyes respond to single photons,12) although the retina does not seem to send a signal to the brain until close to 10 photons have been detected. The sense of smell might partially identify molecules by their vibrational modes excited by inelastic electron tunneling,13) although this is disputed.
Biological settings are not places where you would expect quantum coherence to persist for very long. They have too high temperatures and lots of complex interactions. However, there are a few examples of quantum coherence persisting for much larger time or length scales than we would naively think is possible. Additionally, sensory organs can detect and respond to extremely small signals.
We do not know of any evidence that something similar happens somewhere in the human brain. A few scholars have suggested that microtubules are involved.14)
It seems as though there are instances where macromolecules amplify quantum effects to larger length or time scales. The most interesting effects would occur if quantum coherence was amplified to macroscopic scales. Alternatively, quantum effects could act more simply as a random number generator. In either case, if chaos at larger scales continues to amplify this uncertainty, it can make the brain’s future behavior inherently unpredictable.
Cells
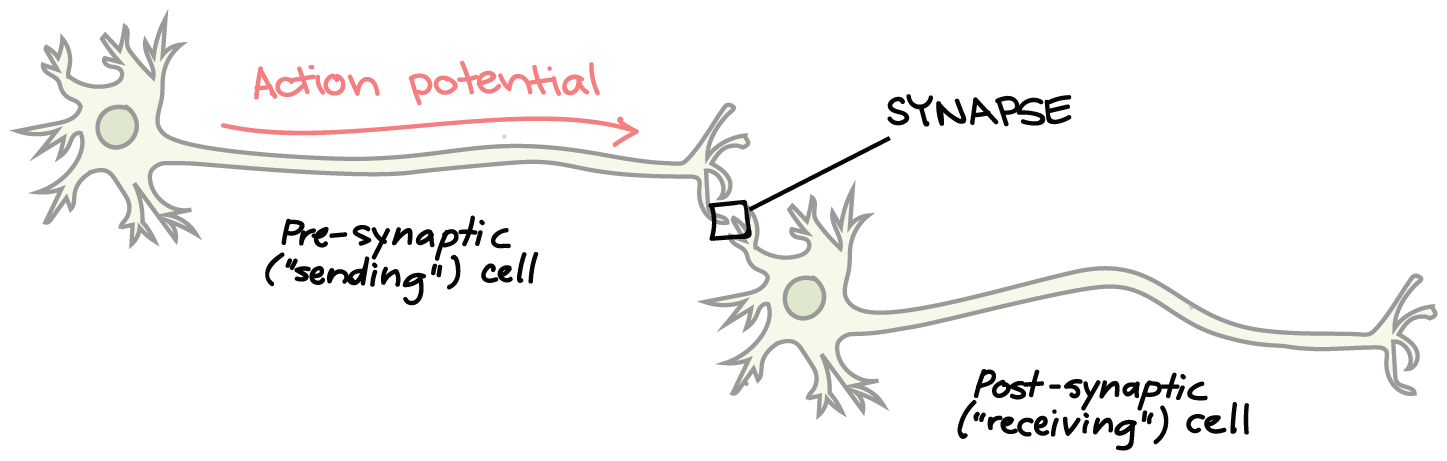
Neurons are a type of cell in the brain which process information. Neurons are connected in large networks which act collectively to produce behavior. The way they are connected is through synapses, small junctions in between two neurons where neurotransmitters can be exchanged.
When neurotransmitters are released at synaptic junctions, they can bind to receptors embedded in the neuron's cell wall. If the receptors are activated by the neurotransmitters, they open and allow an influx of potassium and sodium ions (both positively charged) into the cell, which causes a spike in the neuron's internal voltage. If that voltage passes a threshold, an action potential is fired. An action potential then travels down the axon of a neuron, causing the synapses of that neuron to release neurotransmitters to the next neuron, and the cycle repeats (shown below).
Figure 1: A drawing of two interacting neurons.15)
The best experiments on the dynamics of a single neuron seem to involve the squid giant axon. It is unusually large, with a diameter of about 0.5 mm, which makes it much easier to do experiments with.
By experimentally varying the voltage across the cell membrane and the concentration of ions on either side, Hodgkin & Huxley derived equations of motion for the ion channel in a localized patch.16) This model involves a differential equation with four variables. It can exhibit steady, periodic, or chaotic motion, with transitions between the different types of motion. Similar behavior can be seen in their experiments, although some of the electrical or chemical stimulations were far from being physiologically realistic.
While the Hodgkin-Huxley model was originally for a single patch of the cell membrane, introducing interaction terms between neighboring patches allows it to model the propagation of a signal along the axon. Hindmarsh and Rose reduced this model to a three variable differential equation for the neuron as a whole.17) It also shows bifurcations, bistable behavior, and chaos. Often, the model will show the neurons firing in bursts, with long quiescent periods in between.
Several other experiments on single neurons have also exhibited chaos. Individual buccal-oral neurons of the sea slug Pleurobranchae californica showed evidence of chaos, although the time series was short and non-stationary,18) while the K15 neuron of another mollusc Aplysia californica showed bistablility and irregular & bursting firing patterns.19) The anterior burster neuron of the stomatogastric ganglion of the spiny lobster Pancibirus interruptus operates close to a bifurcation point which allows it to transition between periodic and chaotic motion.20) Individual neurons also seem to be capable of distinguishing between chaotic and stochastic signals: sensory neurons from a rat’s skin showed observably different patterns of spikes in response to a stochastic input, compared to an input derived from the Rössler equations.21)
It seems pretty common, both in theoretical models and in experiments, for individual neurons to behave chaotically. Chaos does not just occur in pathological conditions or environments far from physiologically realistic: individual neurons can behave chaotically in conditions similar to those in living organisms. This suggests that the normal behavior of neurons sometimes makes use of the chaotic behavior which can occur in individual cells. The observation that individual neurons can distinguish between chaotic and stochastic signals further suggests that chaotic behavior is important, because if it were not, there would be no reason for neurons to have this ability.
Small Networks of Neurons
Connections between neurons are often more important than the behavior of the neurons themselves. The connections involve which neurons are connected to which others, whether the connection is excitatory or inhibitory, and the time scale on which they interact. A particular network can have multiple different functions or behaviors and can substantially modify its function without changing its anatomy.
If the individual neurons are behaving periodically, then the network is a system of coupled nonlinear oscillators. When neurons with different intrinsic frequencies are coupled, they can become synchronized or anti-synchronized, depending on the type of connection.22) Coupled nonlinear oscillators can also result in chaos: the double pendulum is a non-biological example of two nonlinear oscillators (pendula) which are not chaotic individually but become chaotic when coupled. A similar thing was unambiguously seen in guinea pig inferior olivary neurons,23) where the coupled oscillators resulted in a strange attractor with dimension 2.85 and a Lyapunov time of about 5-10 millisecond / bit.24)
The individual neurons can also be chaotic themselves. Sometimes, individual neurons stop being chaotic when connected to a network.25) Other times, the neurons in the network remain chaotic, but become synchronized with each other.26) The interacting chaotic neurons can also result in even more chaos. There can be multiple strange attractors, with rapid transitions between two chaotic states with distinct statistics.27)
Interactions between neurons which can be either periodic or chaotic themselves can result in a network which is itself either periodic or chaotic. The result of the interactions can either be to increase or decrease the amount of chaos in the system. Rapid transitions between any of these possibilities are possible as well.
Neurons in Sense Organs
The neurons in sense organs provide a larger scale network that is easy to manipulate while the neurons are still in the animal. While being unusually easy to access is a good thing for experiments, these networks of neurons might be atypical in other ways too. The “goal” of a sense organ is to convey information from the environment to the brain. We might expect these networks of neurons to be unusually function-like: each external state of the world “should” translate into a particular signal sent to the brain. This suggests that these neurons will be unusually predictable, compared to neurons with other roles. Nevertheless, we do see examples of chaotic behavior in the networks of neurons in sense organs.
Two experiments stand out as particularly good examples of how chaos and transitions to and from chaos can play a role in the nervous system.
When shown a flash of light, the neurons in a retina (of tiger salamander larvae or humans) exhibit a particular firing pattern, which stops shortly after the flash.28) If the flash is shown periodically, with a frequency of less than 9 Hz, the retina’s response is periodic: each flash is followed by this particular firing pattern. When the frequency exceeds 9 Hz, there is not enough time for this pattern to complete, so every other response is different. The retina responds periodically, with a period double the period of the flashing light. When the frequency exceeds 12 Hz, the period doubles again and the retina’s response is the same only after every four flashes. When the frequency exceeds 15 Hz, the retina’s response is chaotic. The subjects say that the light appears “flickering.” This is a period doubling cascade, Feigenbaum’s classic route to chaos.29) Feigenbaum’s theory predicts that, with more precise control over the frequency of the flashing light, you could see the retina respond at 8 or 16 times the period of the flashing light, and that the period doubling bifurcations get closer together in a way characterized by Feigenbaum’s constants, before transitioning to chaos.
The normal firing pattern of neurons in the olfactory bulb of rabbits is chaotic.30) When exposed to a smell the rabbit has previously learned, the firing patterns cease to be chaotic and instead become periodic. The periodic motion seems to follow one of the unstable periodic orbits embedded in the original strange attractor. Each smell the rabbit has previously learned corresponds to a different periodic orbit. It seems as though the olfactory bulb is using a kind of dynamical memory storage, which allows rapid responses to learned stimuli. The smells are remembered as unstable periodic orbits within the strange attractor.
Similar experiments have been done on anesthetized spider monkeys,31) anesthetized rats,32) asleep cats,33) and awake chickens.34) The normal behavior of these sensory neurons seems to be chaotic, and the chaos is altered dramatically in response to a stimulus.
Entire Brain
The human brain is much more complicated and difficult to access than the networks of neurons in sense organs. Our current understanding of how the brain works is extremely limited, in terms of which neurons connect to which other neurons, in terms of how the neurons impact each other, and in terms of what kinds of dynamics result from these interactions.
Central neurons which have lots of presynaptic cells are particularly interesting. The effect of having this many presynaptic cells influencing them is a continuous variation of the membrane potential, called “synaptic noise”.35) This “noise” is likely not simply noise, but instead is a complicated chaotic signal which contains information about various parts of the brain.36) These central neurons seem like they would be particularly good at amplifying smaller scale uncertainties.
One measurement scientists use to study whole brain behavior is EEG (electroencephalogram). Many electrodes are attached to the skull and electrical activity is recorded. This method is not fine-grained enough to capture electrical activity of single neurons; instead each electrode records from millions of neurons at once. Often, even at this coarse-grained level, clear dynamics emerge. For instance, typically there are oscillations of various frequencies in the brain, such as during periods of concentration or sleep.
There is significant disagreement in the literature about whether data from EEGs of normal brain activity exhibit chaos. Some papers show indicators of chaos,37) while others show that similar behavior can arise from certain types of noise.38) If normal EEG readings are chaotic, then the chaos is high dimensional, which means that many variables are needed to characterize the motion. This makes it difficult to reconstruct the state space from a time series. If the normal EEG readings show noise, then it is unclear what the source of the noise is - and one possibility is a hard to characterize chaotic system.39) Either the noise or the chaos seem like significant barriers to predicting the behavior of the brain.
EEG data during an epileptic seizure is much less ambiguous. It is clearly chaotic, with a low enough dimensional strange attractor to be clearly reconstructed using time-delay coordinates.40) Chaos theory can help predict these seizures: the measured Lyapunov exponent, averaged over the time series, starts to fall about minutes before the onset of the seizure.41) During the seizure, the Lyapunov time is 0.3-0.5 seconds / bit.42) It seems as though epilepsy is a dynamical disease, characterized by a reduction in the complexity of the dynamics of the brain, from high dimensional chaos/noise to low dimensional chaos.43)
At the scale of the entire brain, there is again a somewhat ambiguous result. There certainly are circumstances where chaos is relevant, but it is hard to tell the extent to which chaos is normal. This is perhaps not surprising to careful students of human behavior. Humans can be both very chaotic and very predictable, with rapid and often unpredictable transitions between the two.
Society
We can zoom out even farther from the scale of an individual human and look at whether human societies are chaotic. This is another area where we have little expertise, and so will not say much. We mostly want to establish that there exists at least some behaviors at scales larger than individual humans which are chaotic.
Some of the clearest evidence for chaos arising from interactions between multiple humans occurs in traffic flows. Traffic can be modeled as a fluid, which allows us to use a broad range of analytical tools originally designed for fluid mechanics. The easiest fluid-like behavior to see while driving is “standing waves”: stop-and-go patterns which develop on highways between interchanges. Although it is not as easy to see while driving, traffic flow rates can also vary chaotically.44) Traffic engineers try to design the road system to avoid these behaviors, and keep the traffic flowing as smoothly as possible.45)
There is some evidence of chaos in financial markets.46) There is reason to be a bit skeptical of these results. Markets seem like intrinsically high dimensional systems where it is hard to distinguish between chaos and noise. They are probably better understood as being anti-inductive. There could be patterns in financial data which are discoverable using techniques from chaos theory. If they were found, someone would likely figure out a way to make money off of them, and the pattern would go away.
Another way to phrase the question of sensitive dependence on initial conditions47) for human societies is: Can a single person have a lasting impact on history? This is a matter of debate among historians, which we will not dig into here.
Much like lower levels, it seems plausible that there are both chaotic and non-chaotic dynamics in human societies, which can change depending on the circumstances and which aspects of society you are investigating.
Conclusion
At every scale, it seems possible for humans to be either chaotic or non-chaotic. In some circumstances, behavior is extremely sensitive to small changes, and small scale uncertainties grow exponentially in time. In other circumstances, the behavior is much more predictable, and small scale uncertainties are corrected for.
When the dynamics is chaotic, it is often non-stationary and multistable. It is not just the details of the future that vary - the qualitative features and statistical properties of the dynamics vary too. Different initial conditions can lead to dramatically different chaotic states - or to states which are not chaotic.
While this is a complicated result, it is perhaps not surprising. There are some aspects of human behavior which we find easy to predict. But people also sometimes behave in surprising ways. This surprise is not just because we are ignorant of the state of our brains. The dynamics of the brain can be inherently unpredictable, at time scales of less than 1 second,48) even with as good of knowledge of the state of the brain as possible. Attempting to completely control a brain would not only involve continual inputs at a frequency of more than 1 / second, it would also require precise microscopic inputs at at least some locations inside of the brain. Completely predicting or controlling the dynamics of a human brain is not possible.
Why would chaos exist in the brain? If there were no advantage to having it, we would expect to see less of it.
One use of chaos has already been discussed: dynamical memory in sense organs (and perhaps elsewhere), where the information is stored as unstable periodic orbits in a strange attractor. This dynamical memory allows a large amount of information to be stored and quickly retrieved in response to a signal.
Other uses of chaos in the brain are more speculative. The simplest use is for chaotic amplification of microscopic uncertainty to act as a random number generator, for circumstances where being unpredictable is advantageous. A few scholars have argued that chaos in the brain allows an organism to respond more quickly and efficiently to rapidly changing and unprecedented circumstances.49) There could also be something going on here with agency and creativity.
Regardless of what chaos in the brain might be useful for, its existence suggests a different way to think of the “software” of the human brain.
In a (classical) computer, there is a non-chaotic mesoscale which shields the macroscopic behavior from microscopic uncertainties. Bits are designed to be either 0 or 1, and to not randomly switch between the two. This renders computers deterministic and re-initializable. The initial state can be fully characterized by the state of each bit, and running the same code on the same initial state gives the exact same result.
In contrast, the human brain does not have a mesoscale which is inherently non-chaotic. It does not seem to make sense to think of neurons as bits, which can be in one of two states (firing or not firing) that change as a result of inputs to the neuron. Instead, the neurons themselves have complex internal dynamics. The “bits” of the brain can be periodic or chaotic in multiple different ways.
Primary authors: Jeffrey Heninger and Aysja Johnson.
Notes
Bak. How Nature Works: The Science of Self-Organised Criticality. (Copernicus Press, New York, 1996).
“One of the best established facts in thermodynamics is that it is impossible in a system enclosed in an envelope which permits neither change of volume nor passage of heat, and in which both the temperature and the pressure are everywhere the same, to produce any inequality of temperature or of pressure without the expenditure of work. This is the second law of thermodynamics, and it is undoubtedly true as long as we can deal with bodies only in mass, and have no power of perceiving or handling the separate molecules of which they are made up. But if we conceive a being whose faculties are so sharpened that he can follow every molecule in its course, such a being, whose attributes are still as essentially finite as our own, would be able to do what is at present impossible to us. …”
Ritz. Quantum effects in biology: Bird navigation. Procedia Chemistry 3. (2011) https://www.sciencedirect.com/science/article/pii/S1876619611000738.
Heninger & Johnson. Chaos and Intrinsic Unpredictability. AI Impacts. http://aiimpacts.org/wp-content/uploads/2023/04/Chaos-and-Intrinsic-Unpredictability.pdf.
See also Wikipedia: Period-doubling bifurcation or Scholarpedia: Period doubling.
Freeman & Di Prisco. Spatial patterns differences with discriminated odors manifest chaotic and limit cycles attractors in olfactory bulb of rabbits. Brain Theory. (1986) p. 97-119.
Pritchard et al. Dimensional analysis of resting human EEG II: Surrogate-data testing indicates nonlinearity but not low-dimensional chaos. Psychophisiology 32.5. (1995) p. 486-491. https://onlinelibrary.wiley.com/doi/abs/10.1111/j.1469-8986.1995.tb02100.x.
Nagatani. Chaotic jam and phase transition in traffic flow with passing. Physical Review E 60. (1999) https://journals.aps.org/pre/abstract/10.1103/PhysRevE.60.1535.
Vaga. Profiting from Chaos: Using Chaos Theory for Market Timing, Stock Selection, and Option Valuation. (1994)